おはようございます、こんにちは、こんばんは、暇物です。
ブログの解説を祝して、1記事したためようという次第です。
2回目があるかはわかりません。
この記事では”厳密にはどうか”といった議論ではなく、”こんな感じに捉えてみるのはいかがでしょうか”という提案を目指します。
教育者としての記事ではなく(そんな自覚は毛頭もありません)、実際に自分が物理を勉強していく中で「あ、こう捉えたらスッキリ」と感じたことの紹介です。率直に物理が(まだ)苦手な人向けです。
(勉強していく中で〜なんて書きましたが、正直に言えばこの記事のコアとなる考え方は友人に教えてもらっただけです。笑)
今日のテーマは以下の通り。
力学は力と運動方程式をかくところから始めよう
ということです。なお、具体的に問題を解くことなどはせず、どう考えるかだけを書きます。
力学とはそもそもなんなのか?
物体間に働く力と運動との関係を研究する物理学の一分野
参照:コトバンク 力学すごくシンプルです。
力が働いたら物が動く。
あるいは、
物が動いているということは力が働いている(た)
それについて調べてみよう。つまり「力と運動の関係を調べてみよう」という分野なわけですね。
力と運動の関係。これあれですよね。そう、運動方程式です。
運動方程式とは
物体の運動を決める微分方程式
参照:コトバンク 運動方程式
あぁ急に難しい。ビブンホウテイシキという呪文はおいておき「物体の運動を決める」に注目してみましょう。
先ほど、力学とは「力と運動の関係を調べてみよう」という分野だと書きました。
そして、運動方程式は「物体の運動を決める」、加速度(運動)と力に関する方程式です。
運動方程式って力学そのものだ、という気がしてきませんか?
力と運動について調べたい分野(力学)に、力と運動について記述してくれる方程式(運動方程式)がある
これを知った時、力学の問題は運動方程式を立てるところから始めて然るべきだ、と思えたんです。
ちなみに微分方程式は関数方程式の一種なので、解くことで関数が得られます。
力学の場合は、時間を変数とした関数(速度や位置)が得られると考えて良いでしょう。
つまり、運動方程式(微分方程式)を解く=運動の様子を表す関数を得られる、ということです。
力学の問題をどう解くか

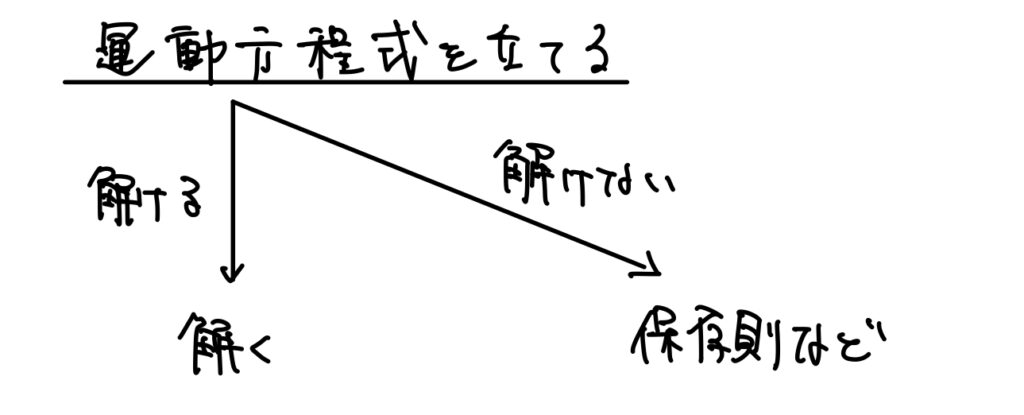
私は力学の問題は大きく以下の2つのパターンに分けられるかなと思います。(大きく分けすぎですが。笑)
というより①のパターンで解きたいけど、解けないから仕方なく②だ、という見方をしています。
①立てた運動方程式が解ける問題
②立てた運動方程式が解けない問題
①②に共通するのはとにかく「運動方程式は立てる」ということです。
そしてそのために「力の図示をする」。この2点は欠かせないわけですね。
⓪力の図示と運動方程式の立式
力の図示について
まず問題文を丁寧に読んで状況把握をしたら力の図示をします。
力の図示の際に私は必ず以下の順番で図示をします。
- 触れていなくても受ける力
重力やクーロン力など、物体同士が触れていなくても受ける摩訶不思議な力です。 - 接触面で受ける力
垂直抗力、摩擦力、衝突の際に働く力(撃力)など。
この時に、一緒に力を書き込みます。例えば、
- 重力なら公式を使ってmg
- 垂直抗力は文字で置いてN
- 動摩擦力は与えられた文字と自分で置いた文字を使ってμ’N
みたいな感じです。(文字はいちいち定義しませんが大概こんな感じでしょう)
運動方程式の立式について
運動方程式の立式は必ず以下の手順で立式をします。
- 座標軸を設定する
多くの問題が平面上の運動の話なのでとりあえずx軸,y軸を設定します。 - 成分ごとに運動方程式を立式
図示した力を見ながら各成分ごとに立式をします。
運動方程式が立ちました。つまり、「物体の運動を決める微分方程式」ができたわけです。
そうです、ここで運動が決まりました。(すごい)
①立てた運動方程式が解ける問題
運動方程式がたった=運動が決まった
ではあとは、運動方程式を解くだけで、運動の記述が完了します。しかしここで問題が生じます。
運動方程式(微分方程式)を解けない場合があるのです。
運動を決める方程式が手に入ったのに、運動の様子を表す式が手に入らない場合があるのは奇妙な気もしますが、飲み込むことにして、まずは運動方程式が解ける問題を考えます。
私たち(高校生など受験に向けた物理を勉強する人)が解ける運動方程式はせいぜい以下でしょう。
- 力が働かない(等速/静止)
- 力が一定(等加速度運動)
- 復元力(単振動)
- 空気抵抗(終端速度がある運動)
(円運動もありますがちょっと除外しておきます)
この場合は運動方程式が解ける=運動の様子が式で表せるのだから解いてしまって設問に答えればOKです。
運動方程式の解き方は以下を見てみてください。
余談)力のつり合いも運動方程式だという話
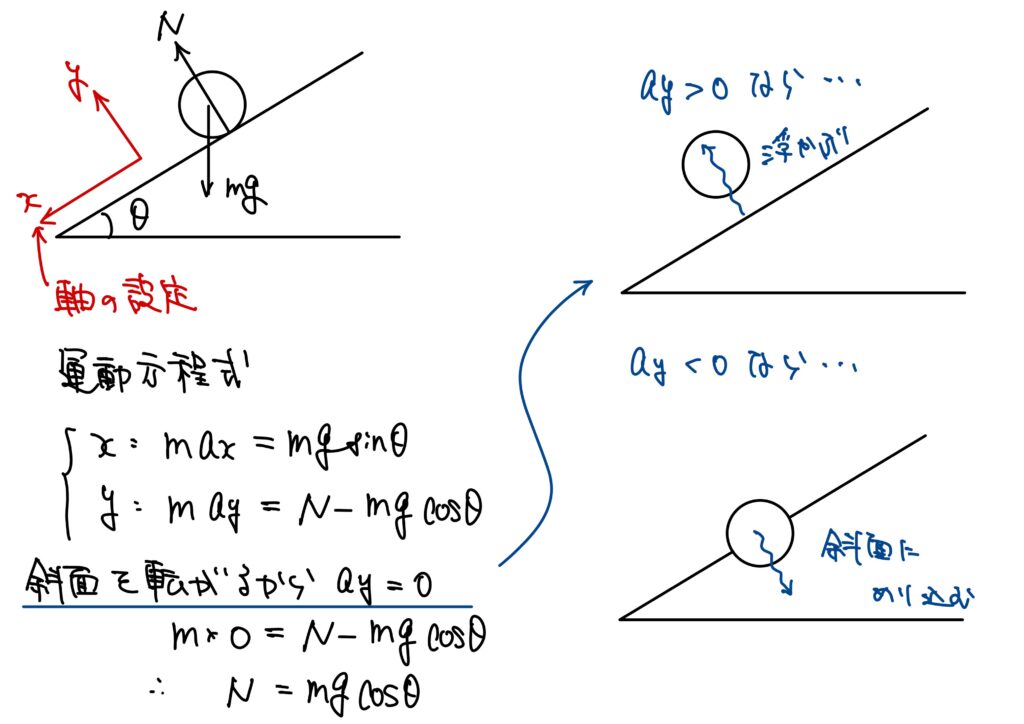
突然例を挙げますが、垂直抗力を求める時、力のつり合いを考えてN=mg(あるいはN=mgcosθ)と書く人も多いかと思います。(結果を覚えている人もいるでしょうね)
これは、立式した運動方程式に加速度0を入れた結果、求まる値です。
(イメージ)
②立てた運動方程式が解けない問題
運動方程式が解けない=運動の様子を定められない
ということです。困りました。では問題は解けないのかというとそうではありません。
当たり前ですが必ず解けるような設定をくれているわけです。
よくある設定は以下のような感じでしょうか
- 完全弾性衝突をする(運動量と力学的エネルギーが保存)
- 反発係数eで衝突(運動量が保存し、反発係数から前後の速度の関係がわかる)
- 外部から力を受けない(力学的エネルギーが保存)
- 外部からある既知の力が与えられる(仕事とエネルギーの関係)
いずれの場合も、運動の詳細を記述する関数(=運動方程式の解)を得ることはできないが、どういうわけか知りたい時点の運動については記述できてしまう、というような感じです。
できるなら運動方程式を解きたい!
ここまでの話をまとめると、
運動方程式を解くことができる問題は、あらゆる時間の運動を記述する関数が得られる。
つまり、あらゆる時間の運動を記述できたことになります。(外部から何か操作が新たに加わらなければ)
一方で、運動方程式を解くことができない問題は、あらゆる時間の運動は記述できないが、ある一時と一時点の比較からその瞬間だけは運動の様子がわかるというような感じです。(往々にして初期の状態と問われている瞬間の比較をしますね)
だったらできれば運動方程式を解きたくないですか?だって、全部の時間の運動がわかるから。
なので、力学の問題は(特に慣れないうちは)とにかく力を図示して運動方程式を立てるのがいいのではないか?と思っています。その後、
- 運動方程式が解ける→解いて答える
- 運動方程式が解けない→諦めて他の条件から答えを得る
というふうな分岐になるかなと思っています。
運動方程式を解けるが解かないで良い場合もある
運動方程式を解ける問題でも、保存則などを用いることで正答に辿り着くことができる問題はたくさんあります。ただ、その場合にも「運動方程式解けるけど、保存則のほうが早いから」といったような意識を持てるようになるといいなと思っています。
ちなみに、私が難系の問題を解く際には、可能な限り運動方程式を解く方針を採用しています。特に単振動の分野などはその傾向を見て取れるかと思います。
もちろん、どちらのどんどん慣れてきたら試験に向けて“なるべく短時間で正答を得られる解き方”で解けるようになる方がいいですけどね。
余談)保存則は運動方程式から導かれる
運動量保存則、力学的エネルギー保存則、仕事とエネルギーの関係などは実は全て運動方程式から導けます。よく”微積物理”とか言われているやつはこういうやつですね。
実際、この導出がわかっていると運動方程式を見れば、
「あ、この2体はx方向の運動量が保存するな」
とわかるようになります。
・運動量保存は系に外力が作用しない時に成立
・物体の運動方程式の和を取ると右辺が0になる時、運動量保存が成立する
上記は同じことを言っているのですが、言葉としての理解と、数式の見た目としての理解が両方できていると「たまたま思いつかなかった」という事態を避けられるのでいいなと思います。
誰かのためになったらいいな
私はもともと物理が大の苦手だったのですが、物理が得意な友人に上記のようなことを教えてもらってから、急に頭がスッキリして「すっごい面白いかも」と思うようになりました。
たまたま彼がいたから物理を好きになったので、私の記事をたまたま読んだ誰かが同じように感じてくれたら嬉しいです。
 Xでシェアする
Xでシェアする
No responses yet